直角三角形で最も有名な公式である三平方の定理(ピタゴラスの定理)は中学3年の数学で学習します。 次に、4つある直角三角形のひとつを考えます。 ・正方形の中に内接する正方形を描く。 2点間の距離を求めなさい。三角形重心定理重心的性质 编辑 1、重心到顶点的距离是重心到 对边 中点的距离的2倍。 2、重心和三角形3个顶点组成的3个三角形面积相等。 即重心到三条边的距离与三条边的长成反比。 3、重心到三角形3个顶点距离的平方和最小。 4、在 平面直角坐标系中3数学 三平方の定理 三辺の長さから三角形の面積を求める 9cm 10cm 11cm A B C x y D 頂点Aから辺BCに垂線をおろしその交点をDとする。

三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも
三角形 三平方の定理 証明
三角形 三平方の定理 証明-③利用三角形内角和定理求第三个角 例3在 ABC中,已知 , , ,求b及A 解析由题意得 , , 4、已知三边解三角形 已知三角形的三边a,b,c,解三角形的步骤: ①利用余弦定理求出一个角; ②由正弦定理及 求其他两个角 例4在 ABC中,已知 , , ,求最大角和 几何课关于三角形你不得不记住的定理:从勾股定理到托勒密定理 直角三角形的两条直角边的平方和等于斜边的平方。 也叫毕达哥拉斯定理。 表达式为a b =c 。 在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边




三平方の定理の応用
答:在一个直角三角形中两直角边的平方和等于斜边的平方 问题2 如果一个三角形中有两边的平方和等于第三边的平方,那么这个三角形是否就是直角三角形呢? 合作探究 下面有三组数分别是一个三角形的三边长a,b,c ①5,12,13;左の直角三角形が正三角形を半分にしたものです。 3 3 辺の比は暗記で、 21√3 2 1 3 です。 次に、右の直角三角形に三平方の定理を使うと、 最後の 1 1 辺の長さが求まります。 最後の 1 1 辺の長さを y y とすると y2 =102 y 2 8 2 = 10 2 y2 64 = 100 y 2 64 3分でわかる!二等辺三角形の2つの定理・性質 二等辺三角形の性質・定理ってなに?? こんにちは!この記事をかいているKenだよ。馬、うまいね。 二等辺三角形って、 2つの辺が等しい三角形のこと だったよね?? 名前はかっこいいし、 ルックルも、いい。
如上面的三角形abc内切圆图所示,对三角形abc进行分割,其面积可以分成三个小三角形面积之和,即: 记 为公式五。 在内切圆图中,有 , , ,带入公式五中,则有: 记为公式六。 内切圆是由三角形的三条角平分线的交点所得来的,它和外接圆一样是一个三角形唯一的一个属性,因此也就成了座標上での2点間の 三平方の定理とは、直角三角形の三辺の長さに関する定理である。 斜辺の2乗は他の2辺の2乗の和に等しくなる。 三角形の三辺をa,b,cとし、斜辺がcとするとc^2=a^2b^2となる。三角形三条中位线逆定理,三角形三条中位线逆定理3楼证明有漏洞。de‖bc?理由不充分,用相似形还缺少条件。 可以证明的,用反证法。条件如3楼所设,则 证明:假设de不平行于bc,过b点做bf‖de交ac于点f,则b、f、c三点构成三角形,所以bf≠bc。 但是de是
所以,三角形、勾股定理 反过来也是对的;如果"一个三角形两边的平方和等于第三边的平方,则该三角形为直角三角形"。 西方古代的这个数学家发现这个定理,宰百头牛,举办"百牛宴"进行庆贺,曾将这个定理称为"百牛定理"。 三角形的三边关系定理:三角形第三边小于两边之和,大于两边之差。可以表示为两边之差<第三边<两边之和。 三角形的三边关系定理 设三边为a,b,c,则有 ab>c ac>b bc>a 三边关系推论:a>bc c>ba b>ac 三角形三边关系定理及推论的作用 勾股定理直角三角形中直角边的平方和等于斜边的平方和 正弦定理在一个三角形中,各边和它所对角的正弦的比相等,这就叫做正弦定理 余弦定理余弦 cosα= (B^2C^2A^2)/2BC cosb= (A^2C^2B^2)/2AC cosc= (A^2B^2C^2)/2AB 定理 三角形两边的和大于第三边 推论 三角形




Mathematics 三平方の定理 3 いろいろな三角形 働きアリ




三平方の定理の証明と使い方
中线定理 (pappus定理),又称 重心定理 ,是 欧氏几何 的定理,表述三角形三边和中线长度关系。 定理内容:三角形一条中线两侧所对边平方的和等于底边的平方的一半加上这条中线的平方的2倍。検索語:三角比 三角関数の加法定理 三角比の三角形への応用 オイラー線の傾き 1 はじめに 高校数学「数学i」において三角比および三 角形などへの応用について学習する。応用の内 容は大体,正弦定理,余弦定理,三角形の解法,モーリーの定理とは、三角形に関する幾何学の定理である。 19年にアメリカの数学者{{仮リンクフランク・モーリーenFrank Morley}によって証明された。 概要 任意の三角形においてそれぞれの内角の三等分線を引く。 各辺に近い線同士の交点を P, Q, R とすると、三角形PQR は正三角形になる。




なぜ 三平方の定理で角度bが90度だとわかるのですか Clear




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
中线定理(Apollonius's theorem),又称阿波罗尼奥斯定理,是欧氏几何的定理,表述三角形三边和中线长度关系。 定理内容 三角形一条中线两侧所对边平方和等于底边的一半平方与该边中线平方和的2倍。 定理公式この記事は「平方数」、「三角数」、「多角数定理」などの補遺に当たる。 ここに示す事実は古くから知られている ものであるが呼びかたが定まっていない。 日本語では「三平方和定理」などと呼ばれることもあるが、ピタゴラスの定理とは全く別のものである。 3平方の定理を直角三角形の角度動かし文字式で表現、Excelの図形挿入を使用 直角三角形の角度を90度ずつ動かし、左の図のように長辺の頂点二つを異なるように並べます。すると、 1辺が(XY)の正方形が外側にでき、面積は(XY)²① です。
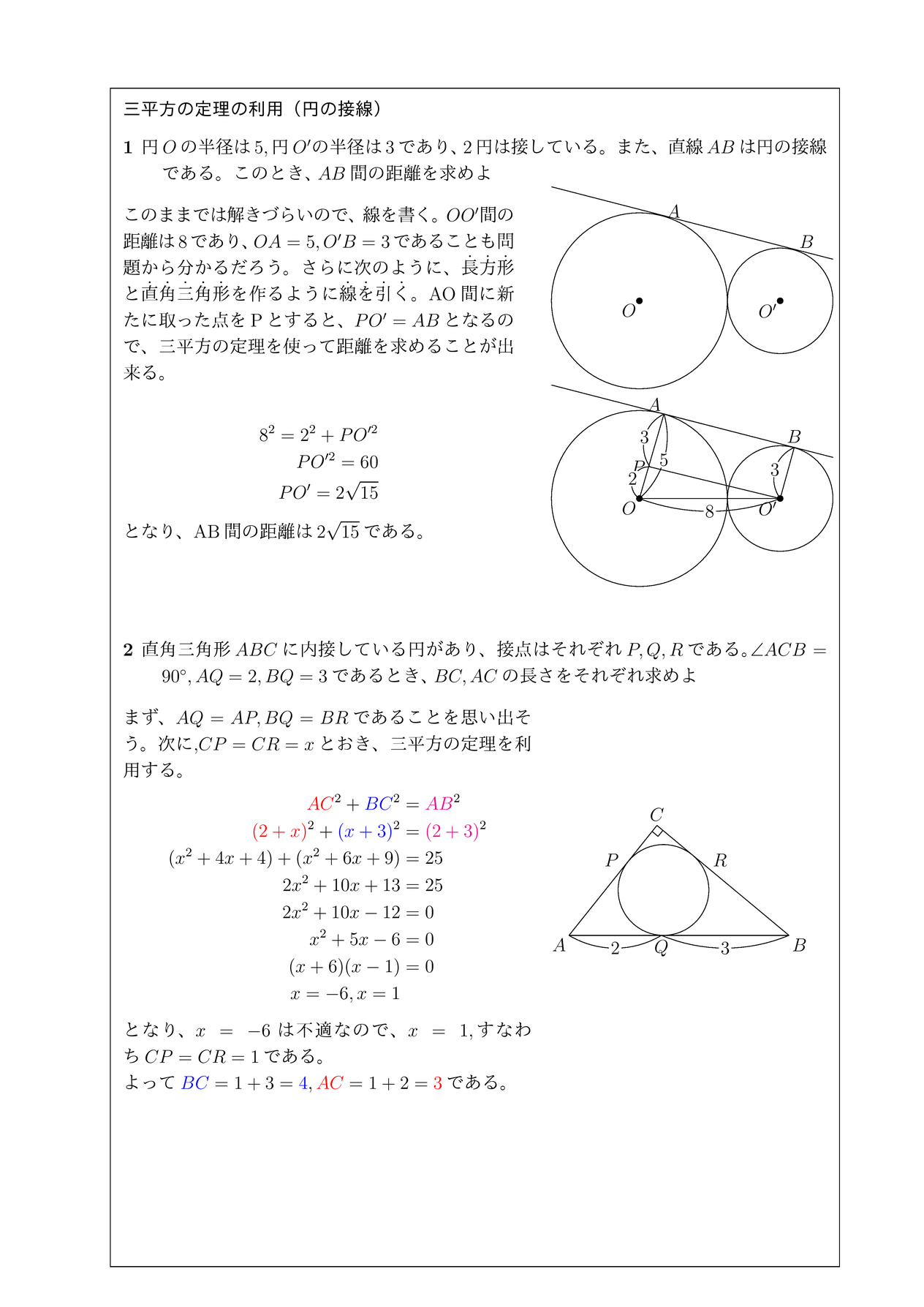



三平方の定理の利用 円の接線 チーム エン




中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su
三角形の合同条件・決定条件には、この他「3 加法定理 と三角 三辺の長さが解って角度を出したいと思ったのですがこの式をそのまま自分の思い描いている式と答えを出すにはだいぶ時間がかかると思いますが少しだけ理解できたのかもしれません日本大百科全書(ニッポニカ) 三平方の定理の用語解説 直角三角形abcが与えられたとき、斜辺bcを1辺とする正方形の面積は、他の2辺ab、acを1辺とする二つの正方形の面積の和に等しい。 三 平方 の 定理 証明 等 積 変形😔 これで、三平方の定理を証明することができました!「平方」とは 2乗のことなので、「三平方の定理」と言われるゆえんは、直角三角形の「三」つの辺それぞれの「平方」、つまり a 2, b 2, c 2 の間に成り立つ関係式ということですね。 14




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ
1 勾股定理(毕达哥拉斯定理) 2射影定理(欧几里得定理) 在rt abc中,∠acb=90°,cd是斜边ab上的高,则有射影定理如下:①cd2=ad·db②bc2=bd·ba③ac2=ad·ab④ac·bc=ab·cd(等积式,可用面积来证明) 3三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分 4 三平方の定理とは 直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思います Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 まとめ三平方の定理ピタゴラスの定理を使えば直角三角形の辺の長さは大体わかる 三平方の定理で直角三角形の辺の長さを求める問題はどうだった 今日勉強した問題のパターンは4つだったな 超基本タイプ




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




三平方の定理と二等辺三角形 Youtube
三角形的三边关系定理 a b c 利用"两点之间,线段最短。 "有:abbc>ac bcac>ab abac>bc 由此得出结论:三角形任意两边之和都大于第三边。 变形得:acbc三平方の定理(ピタゴラスの定理)の証明まとめ5選全部で 三平方の定理 特別な直角三角形の3辺の比|中学生からの 数学三平方の定理が成り立つ三辺の比:最重要7パターン お願いします。三平方の定理が成り立つ3つの整数の組を教えて勾股定理直角三角形中直角边的平方和等于斜边的平方和 正弦定理在一个三角形中,各边和它所对角的正弦的比相等,这就叫做正弦定理 余弦定理余弦 cosα=(B^2C^2A^2)/2BC cosb=(A^2C^2B^2)/2AC cosc=(A^2B^2C^2)/2AB 定理 三角形两边的和大于第三边 推论 三角形




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 自動計算サイト
三角数定理の証明に用いる定理を紹介します。 8 8 8 で割って 3 3 3 余る正の整数は三つ以下の平方数の和で表せる (ルジャンドルの結果の特殊な場合) 三 平方 の 定理 直角 三角形 2月 16, 21 直角三角形において、「直角」をはさむ2つの辺の長さを \ (a,b\)、斜辺の長さを \ (c\) としたとき 三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵|アタリマエ! 写真の三角形の面積を3平方の定理を使って教えてください。 数学 教えて!goo




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理で辺を求める Youtube



1




三平方の定理の応用




三平方の定理 おやじさん ネット



1
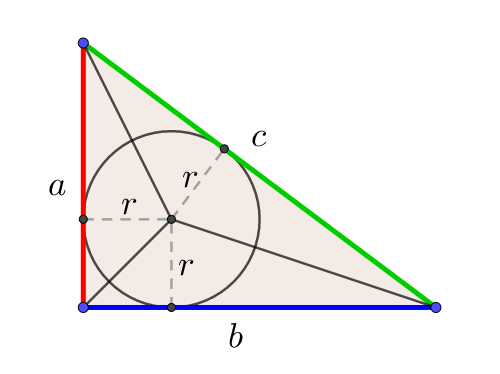



三平方の定理の証明4 直角三角形と内接円 キソカラ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理 特別な直角三角形 イ弋マ本ゼミナール




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ
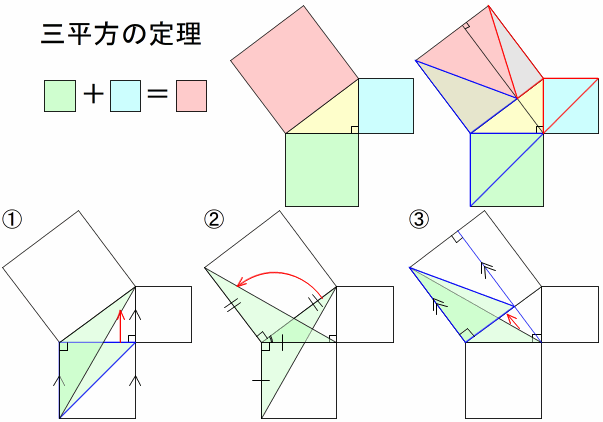



3 4 5の三角形で 本当に直角ができる Note Board




3 4 5の三角形で 本当に直角ができる Note Board




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




三平方の定理の練習問題10問 解き方の解説 数学fun



Studydoctor特別な三角形と三平方の定理 中学3年数学 Studydoctor




三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく



Studydoctor三平方の定理と色々な三角形の面積 中学3年数学 Studydoctor



三平方の定理



1




1999 号 三平方の定理用教材 Astamuse




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張
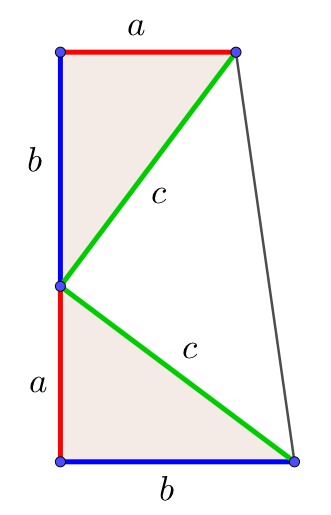



三平方の定理の証明3 大統領の台形 キソカラ
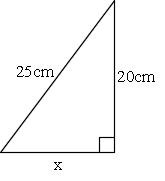



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理の逆ってなに どうやって証明するの 数スタ
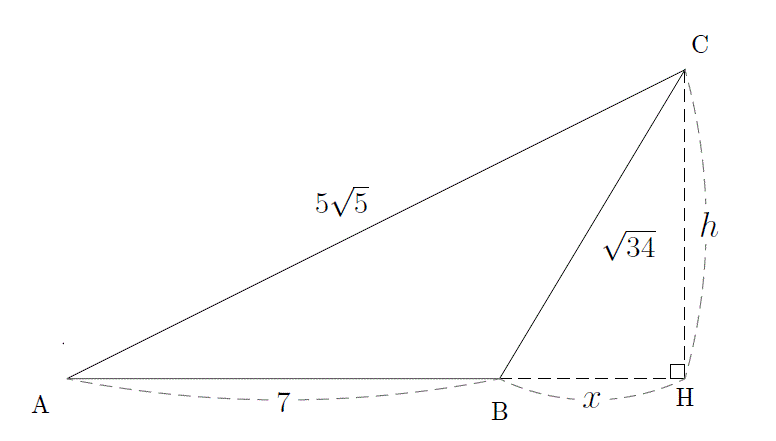



かみのドリル 三平方の定理



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




山と数学 そして英語 三平方の定理と三角形の面積 さらに三角比 ヘロンの公式




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド
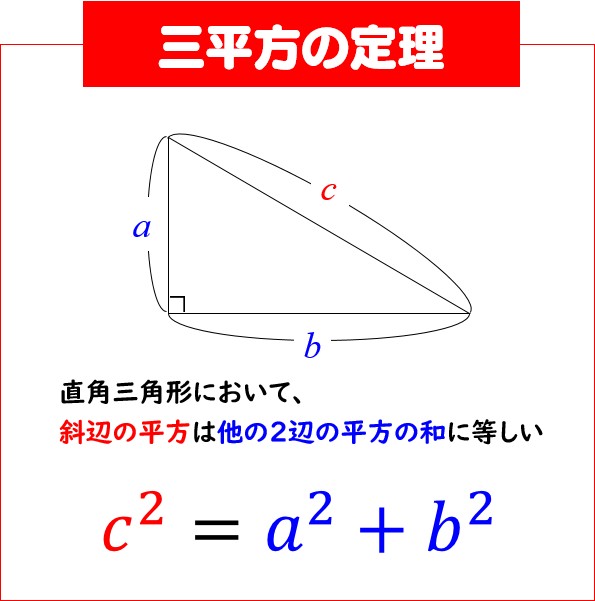



三平方の定理の証明 直感的に分かる図で解説します 数学fun




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




3分で理解 三平方の定理 ピタゴラスの定理 とその証明を完全解説 Rikeinvest




三平方の定理の利用 四角錐 円錐 チーム エン
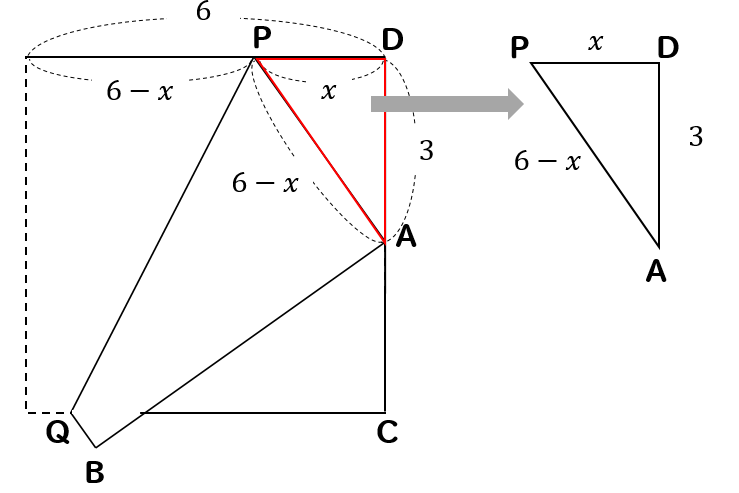



三平方の定理 方程式を利用する発展問題を解説 数スタ




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト




三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト




三平方の定理 無料で使える中学学習プリント




三平方の定理2
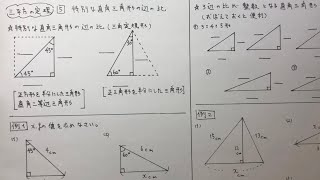



中3数学 三平方の定理5 特別な直角三角形の辺の比 すべて無料 星組の中学数学講座




Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学




三平方の定理です この Abcの高さahと面積の求め方を教えてください Clear



三平方の定理




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理の証明と使い方




中学数学 三平方の定理 30 60 90 の直角三角形 オンライン無料塾 ターンナップ




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




中学数学 三平方の定理 30 60 90 の直角三角形 オンライン無料塾 ターンナップ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




國三 Junior High数学的 数学 三平方の定理 筆記 Clear




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




三平方の定理の拡張について考えよう 理科好き子供の広場




三平方の定理の証明 方べきの定理の利用1 Fukusukeの数学めも



三平方の定理
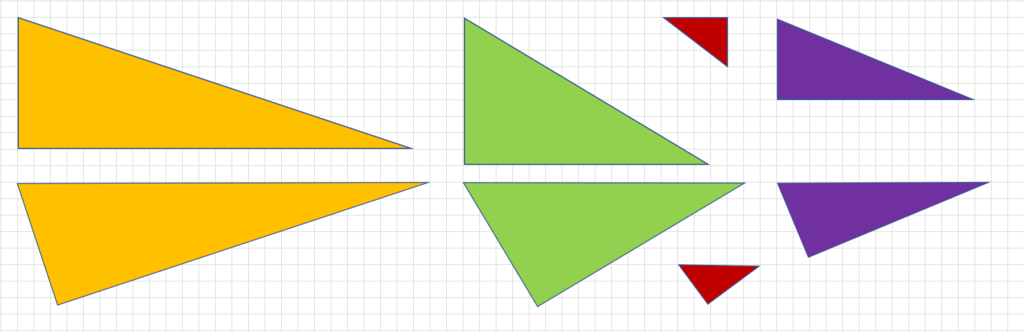



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori
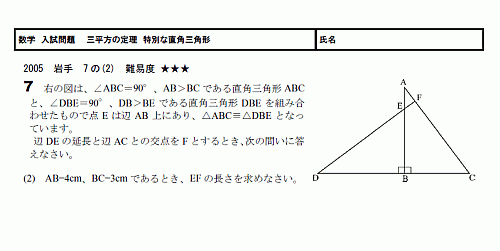



三平方の定理 スタディーx




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




中学数学 三平方の定理




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
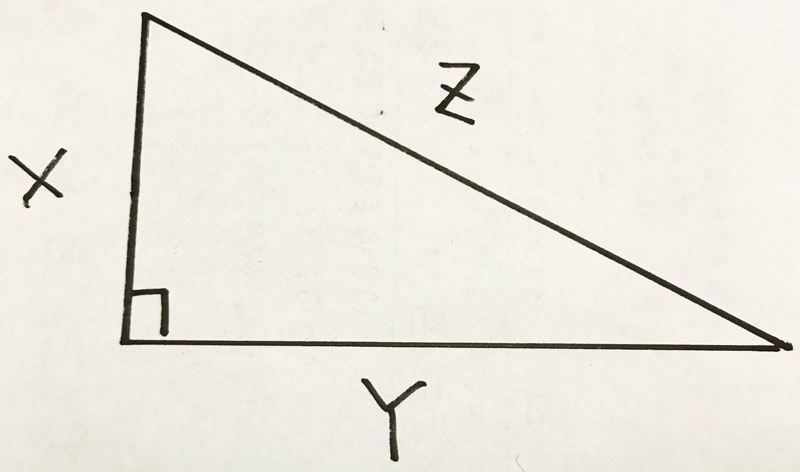



水平線までの距離 三平方の定理 21 3 19 茨木の法律相談 弁護士法人茨木太陽
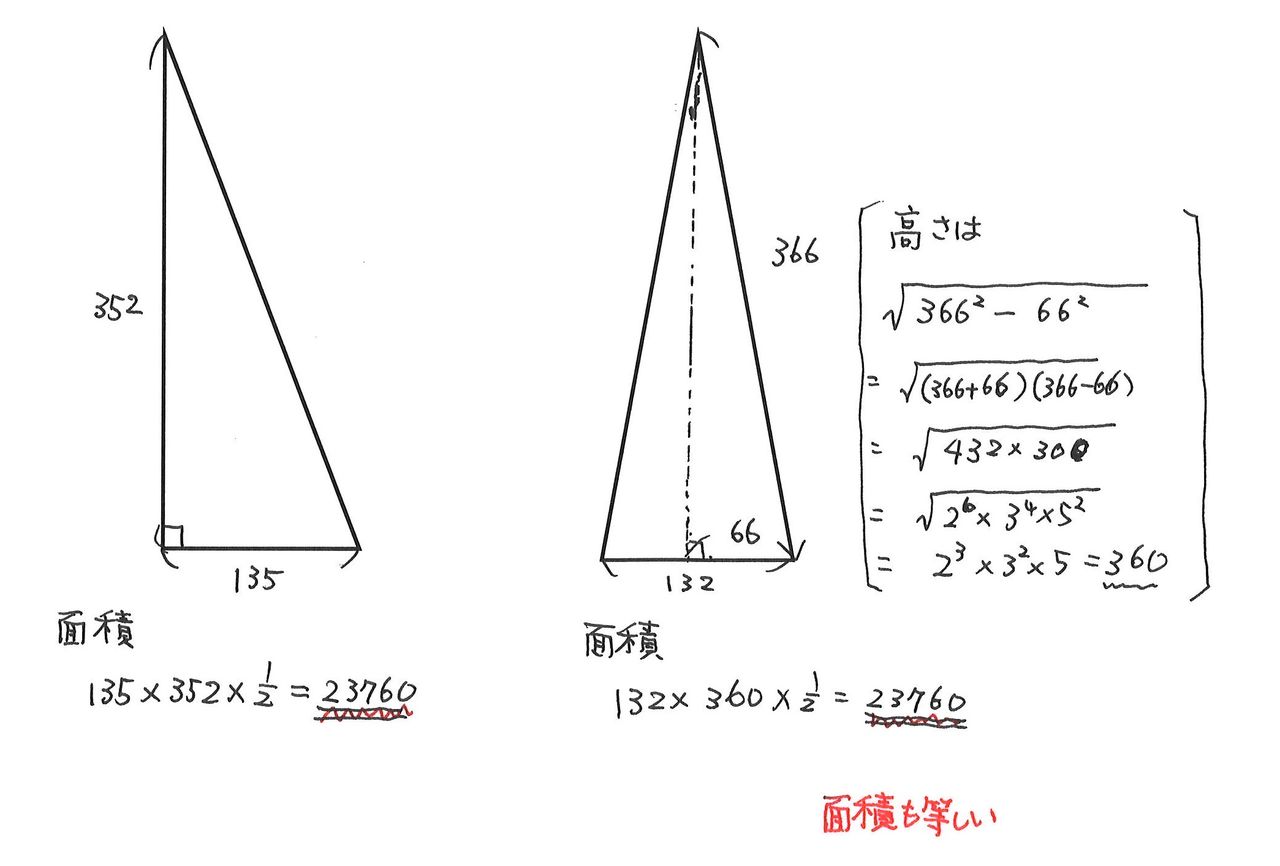



三角形のペア 大田 桐光本部校 ブログ




数学 中3 61 三平方の定理 基本編 Youtube



高校入試 英語 数学 三平方の定理の逆




三平方の定理の証明と使い方



1
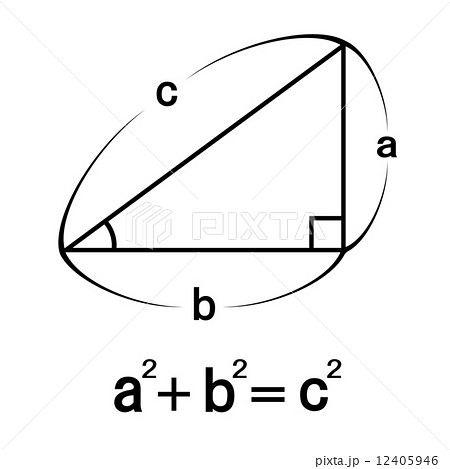



三平方の定理のイラスト素材



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿